A ΔPQR, given that QR = 3 cm,

Given, inv $\triangle P Q R, Q R=3 \mathrm{~cm}, \angle P Q R=45^{\circ}$

and $Q P-P R=2 \mathrm{~cm}$

since, $C$ lies on the perpendicular bisector $R S$ of $A Y$.

To construct $\triangle P Q R$, use the following steps.

1. Draw the base $Q R$ of length $3 \mathrm{~cm}$.

2. Make an angle $X Q R=45^{\circ}$ at point $Q$ of base $Q R$.

3. Cut the line segment $Q S=Q P-P R=2 \mathrm{~cm}$ from the ray $Q X$.

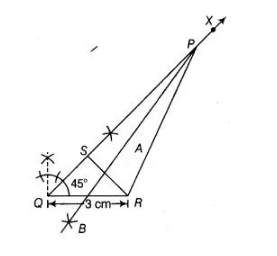
4. Join $S R$ and draw the perpendicular bisector of $S R$ say $A B$.

5. Let bisector $A B$ intersect $Q X$ at $P$. Join $P R$ Thus, $\triangle P Q R$ is the required triangle.

Justification

Base $Q R$ and $\angle P Q R$ are drawn as given.

Since, the point P lies on the perpendicular bisector of SR.

$P S=P R$

NOW, $Q S=P Q-P S$

$=P Q-P R$

Thus, our construction is justified.