A prism of refractive index n1 and another prism of refractive index n2 are stuck together (as shown in the figure).
A prism of refractive index $n_{1}$ and another prism of refractive index $\mathrm{n}_{2}$ are stuck together (as shown in the figure). $\mathrm{n}_{1}$ and $\mathrm{n}_{2}$ depend on $\lambda$, the wavelength of light, according to the relation
$\mathrm{n}_{1}=1.2+\frac{10.8 \times 10^{-14}}{\lambda^{2}}$ and $\mathrm{n}_{2}=1.45+\frac{1.8 \times 10^{-14}}{\lambda^{2}}$
The wavelength for which rays incident at any angle on the interface BC pass through without bending at that interface will be _________ nm.
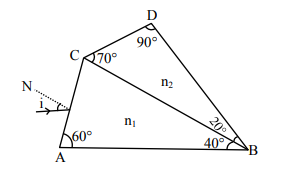
For no bending, $\mathrm{n}_{1}=\mathrm{n}_{2}$
$1.2+\frac{10.8 \times 10^{-14}}{\lambda^{2}}=1.45+\frac{1.8 \times 10^{-4}}{\lambda^{2}}$
On solving,
$9 \times 10^{-14}=25 \lambda^{2}$
$\lambda=6 \times 10^{-7}$
$\lambda=600 \mathrm{~nm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
