A rhombus shaped field has green grass for 18 cows to graze.

Solution:



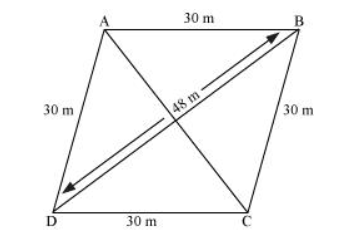
Let ABCD be a rhombus-shaped field.

For $\triangle B C D$,

Semi-perimeter, $s=\frac{(48+30+30) \mathrm{cm}}{2}=54 \mathrm{~m}$

By Heron’s formula,

Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$

Therefore, area of $\triangle B C D=[\sqrt{54(54-48)(54-30)(54-30)}] \mathrm{m}^{2}$

$=\sqrt{54(6)(24)(24)}=3 \times 6 \times 24=432 \mathrm{~m}^{2}$

Area of field $=2 \times$ Area of $\triangle B C D$

$=(2 \times 432) \mathrm{m}^{2}=864 \mathrm{~m}^{2}$

Area for grazing for 1 cow $=\frac{864}{18}=48 \mathrm{~m}^{2}$

Each cow will get $48 \mathrm{~m}^{2}$ area of grass field.