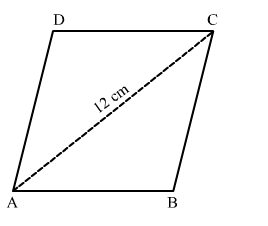
A rhombus-shaped sheet with perimeter 40 cm and one diagonal 12 cm,

Let the sides of rhombus be of length x cm.

Perimeter of rhombus = 4x
⇒ 40 = 4x
⇒ x = 10 cm

Now,
In ∆ABC,
The sides of the triangle are of length 10 cm, 10 cm and 12 cm.
∴ Semi-perimeter of the triangle is

$s=\frac{10+10+12}{2}=\frac{32}{2}=16 \mathrm{~cm}$

∴ By Heron's formula,

Area of $\Delta A B C=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{16(16-10)(16-10)(16-12)}$

$=\sqrt{16(6)(6)(4)}$

$=48 \mathrm{~cm}^{2} \quad \ldots(1)$

In ∆ADC,
The sides of the triangle are of length 10 cm, 10 cm and 12 cm.
∴ Semi-perimeter of the triangle is

$s=\frac{10+10+12}{2}=\frac{32}{2}=16 \mathrm{~cm}$

∴ By Heron's formula,

Area of $\Delta A D C=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{16(16-10)(16-10)(16-12)}$

$=\sqrt{16(6)(6)(4)}$

$=48 \mathrm{~cm}^{2} \quad \ldots(2)$

∴ Area of the rhombus = Area of ∆ABC + Area of ∆ADC
= 48 + 48
= 96 cm2

The cost to paint per cm2 = Rs 5
The cost to paint 96 cm2 = Rs 5 × 96
 = Rs 480
The cost to paint both sides of the sheet = Rs 2 × 480
 = Rs 960

Hence, the total cost of painting is Rs 960.