A right angled triangle with sides 3 cm and 4 cm

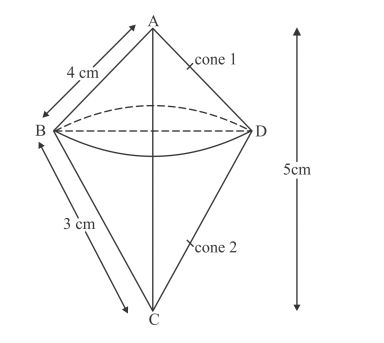
The double cone so formed is as in figure.

Hypotenuse AC

$=\sqrt{3^{2}+4^{2}}$

$=5 \mathrm{~cm} .$

Area of $=\frac{1}{3} \times \frac{22}{7} \times \frac{12}{5} \times \frac{12}{5} \times 5$

$=\frac{1056}{35}$

$=30 \frac{6}{35}$

$\triangle A B C=\frac{1}{2} \times A B \times A C$

$=\frac{1}{2} \times A C \times O B$

$=\frac{1}{2} \times 4 \times 3$

$=\frac{1}{2} \times 5 \times O B$

$=6$

$\frac{1}{2} \times 3 \times 4=\frac{1}{2} \times 5 \times O B$

$O B=\frac{12}{5}$

Volume of double cone = volume of cone 1 + cone 2

$=\frac{1}{3} \pi r^{2} h_{1}+\frac{1}{3} \pi r^{2} h_{2}$

$=\frac{1}{3} \pi r^{2}\left(h_{1}+h_{2}\right)$

$=\frac{1}{3} \pi r^{2}(O A+O C)$

$=\frac{1}{3} \times \frac{22}{7} \times \frac{12}{5} \times \frac{12}{5} \times 5$

$=\frac{1056}{35}$

$=30 \frac{6}{35} \mathrm{~cm}^{2}$