Question.
A right circular cylinder just encloses a sphere of radius r (see figure). Find
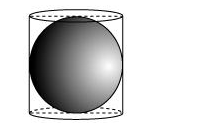
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in (i) and (ii).

(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in (i) and (ii).
Solution:
(i) Surface area of sphere $=4 \pi r^{2}$
(ii) Height of cylinder $=r+r=2 r$
Radius of cylinder $=r$
CSA of cylinder $=2 \pi r h$
$=2 \pi r(2 r)$
$=4 \pi r^{2}$
(iii) Required ratio $=\frac{\text { Surface area of sphere }}{\text { CSA of cylinder }}$
$=\frac{4 \pi r^{2}}{4 \pi r^{2}}$
$=\frac{1}{1}$
Therefore, the ratio between these two surface areas is $1: 1$.

(i) Surface area of sphere $=4 \pi r^{2}$
(ii) Height of cylinder $=r+r=2 r$
Radius of cylinder $=r$
CSA of cylinder $=2 \pi r h$
$=2 \pi r(2 r)$
$=4 \pi r^{2}$
(iii) Required ratio $=\frac{\text { Surface area of sphere }}{\text { CSA of cylinder }}$
$=\frac{4 \pi r^{2}}{4 \pi r^{2}}$
$=\frac{1}{1}$
Therefore, the ratio between these two surface areas is $1: 1$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
