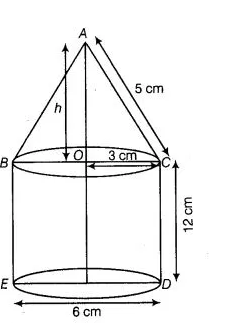
A rocket is in the form of a right circular cylinder

Since, rocket is the combination of a right circular cylinder and a cone.

Given, diameter of the cylinder = 6 cm

$\therefore \quad$ Radius of the cylinder $=\frac{6}{2}=3 \mathrm{~cm}$

and height of the cylinder $=12 \mathrm{~cm}$

$\therefore$ Volume of the cylinder $=\pi r^{2} h=3.14 \times(3)^{2} \times 12$

$=339.12 \mathrm{~cm}^{3}$

and curved surface area $=2 \pi r h$ 

$=2 \times 3.14 \times 3 \times 12=226.08$

Now, in right angled $\triangle A O C$,

$h=\sqrt{5^{2}-3^{2}}=\sqrt{25-9}=\sqrt{16}=4$

$\therefore$ Height of the cone, $h=4 \mathrm{~cm}$

Radius of the cone, $r=3 \mathrm{~cm}$

Now, volume of the cone

$=\frac{1}{3} \pi r^{2} h=\frac{1}{3} \times 3.14 \times(3)^{2} \times 4$

$=\frac{113.04}{3}=37.68 \mathrm{~cm}^{3}$

and curved surface area $=\pi r l=3.14 \times 3 \times 5=47.1$

Hence, total volume of the rocket

$=33912+37.68=376.8 \mathrm{~cm}^{3}$

and total surface area of the rocket $=C S A$ of cone $+C S A$ of cylinder + Area of base of cylinder

$=47.1+226.08+28.26$

$=301.44 \mathrm{~cm}^{2}$