A rod of length 15 cm moves with its ends always touching the coordinate axes.

Given: A rod of length 15 cm moves with its ends always touching the coordinate axes. A point P on the rod, which is at a distance of 3 cm from the end in contact with the x-axis

Need to find: Find the equation of the locus of a point P

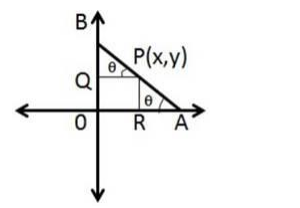
Here AB is the rod making an angle θ with the x-axis

Here AP = 3.

$\mathrm{PB}=\mathrm{AB}-\mathrm{AP}=12-3=9 \mathrm{~cm}$

Here, PQ is the perpendicular drawn from the x-axis and RP is the perpendicular drawn from y-axis.

Let, the coordinates of the point $P$ is $(x, y)$.

Now, in the triangle $\triangle \mathrm{BPQ}$,

$\cos \theta=\frac{x}{P B}=\frac{x}{9}$

And in the triangle $\triangle P A R$,

$\sin \theta=\frac{y}{A P}=\frac{y}{3}$

We know, $\sin ^{2} \theta+\cos ^{2} \theta=1$

$\Rightarrow \frac{x^{2}}{81}+\frac{y^{2}}{9}=1$

This is the locus of the point $P$.