A round table cover has six equal designs as shown in fig.

Solution:

Here, $r=28 \mathrm{~cm} . \theta=\frac{\mathbf{3 6 0}^{\circ}}{\mathbf{6}}=60^{\circ}$

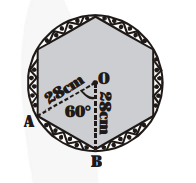
In the figure OAB is equilateral having side 28 cm.

The area of one shaded designed portion

= The area of the sector OAB 

- The area of the $\Delta \mathrm{OAB}$

$=\left\{\frac{60}{360} \times \pi \times(28)^{2}-\frac{\sqrt{3}}{4} \times(28)^{2}\right\} \mathrm{cm}^{2}$$=\left\{\frac{1}{6} \times \frac{22}{7} \times 28 \times 28-\frac{1.7}{4} \times 28 \times 28\right\} \operatorname{cm}^{2}$

$=\left\{\frac{11}{3} \times 112-1.7 \times 196\right\} \mathrm{cm}^{2}$

$=\left\{\frac{1232}{3}-333.2\right\} \mathrm{cm}^{2}$

The total area of six designed portions

$=6 \times\left\{\frac{1232}{3}-333.2\right\} \mathrm{cm}^{2}$

$=2464-1999.2 \mathrm{~cm}^{2}=464.8 \mathrm{~cm}^{2}$

The total cost of making the designs at the rate of Rs $0.35 \mathrm{per} \mathrm{cm}^{2}$

$=$ Rs. $0.35 \times 464.8=$ Rs. $162.68$