A sailor goes 8 km downstream in 40 minutes and returns in 1 hours.

Let the speed of the sailor in still water be x km/hr and the speed of the current be y km/hr

Speed upstream $=(x-y) \mathrm{km} / \mathrm{hr}$

Speed downstream $=(x+y) \mathrm{km} / \mathrm{hr}$

Now, Time taken to cover $8 \mathrm{~km}$ down stream $=\frac{8}{x+y} h r s$

Time taken to cover $8 \mathrm{~km}$ upstream $=\frac{8}{x-y} h r s$

But, time taken to cover $8 \mathrm{~km}$ downstream in 40 minutes or $\frac{40}{60}$ hours that is $\frac{2}{3}$ hours

$\frac{8}{x+y}=\frac{2}{3}$

$8 \times 3=2(x+y)$

$24=2 x+2 y$

Dividing both sides by common factor 2 we get

$12=x+y \cdots(i)$

Time taken to cover 8km upstream in1hour

$\frac{8}{x-y}=1$

$8=1(x-y)$

$8=x-y \quad$...(ii)

By solving these equation $(i)$ and $(i i)$ we get

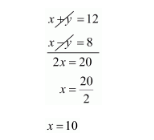
Substitute $x=10$ in equation $(i)$ we get

$x+y=12$

$10+y=12$

$y=12-10$

$y=2$

Hence, the speed of sailor is $10 \mathrm{~km} / \mathrm{hr}$

The speed of current is $2 \mathrm{~km} / \mathrm{hr}$