A sample of pure $\mathrm{PCl}_{5}$ was introduced into an evacuated vessel at $473 \mathrm{~K}$. After equilibrium was attained, concentration of $\mathrm{PCl}_{5}$ was found to be $0.5 \times 10^{-1}$ mol $\mathrm{L}^{-1}$. If value of $K_{c}$ is $8.3 \times 10^{-3}$, what are the concentrations of $\mathrm{PCl}_{3}$ and $\mathrm{Cl}_{2}$ at equilibrium?
$\mathrm{PCl}_{5}(\mathrm{~g}) \longleftrightarrow \mathrm{PCl}_{3}(\mathrm{~g})+\mathrm{Cl}_{2}(\mathrm{~g})$
Let the concentrations of both $\mathrm{PCl}_{3}$ and $\mathrm{Cl}_{2}$ at equilibrium be $x \mathrm{molL}^{-1}$. The given reaction is:
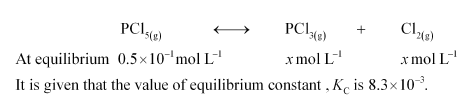
Now we can write the expression for equilibrium as:
$\frac{\left[\mathrm{PCl}_{2}\right]\left[\mathrm{Cl}_{2}\right]}{\left[\mathrm{PCl}_{5}\right]}=K_{\mathrm{C}}$
$\Rightarrow \frac{x \times x}{0.5 \times 10^{-1}}=8.3 \times 10^{-3}$
$\Rightarrow x^{2}=4.15 \times 10^{-4}$
$\Rightarrow x=2.04 \times 10^{-2}$
$=0.0204$
$=0.02($ approximately $)$
Therefore, at equilibrium,
$\left[\mathrm{PCl}_{3}\right]=\left[\mathrm{Cl}_{2}\right]=0.02 \mathrm{~mol} \mathrm{~L}^{-1} .$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.