A satellite is moving in a low nearly circular orbit around the earth. Its radius is roughly equal to that of the earth's radius $R_{e}$. By firing rockets
attached to it, its speed is instantaneously increased in the direction of its motion so that
is become $\sqrt{\frac{3}{2}}$ times larger. Due to this the
farthest distance from the centre of the earth that the satellite reaches is $R$, value of $R$ is :
Correct Option: , 2
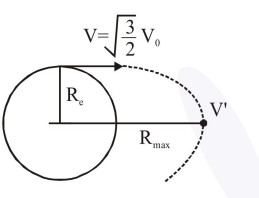
$\mathrm{V}_{0}=\sqrt{\frac{\mathrm{GM}}{\mathrm{R}_{\mathrm{e}}}}$
$\frac{-\mathrm{GMm}}{\mathrm{R}_{e}}+\frac{1}{2} \mathrm{mv}^{2}=\frac{-\mathrm{GMm}}{\mathrm{R}_{\max }}+\frac{1}{2} \mathrm{mv}^{\prime 2}$.$\ldots(i)$
$\mathrm{VR}_{\mathrm{e}}=\mathrm{V}^{\prime} \mathrm{R}_{\max }$....(ii)
Solving (i) & (ii)
$\mathrm{R}_{\max }=3 \mathrm{R}_{\mathrm{e}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.