Question.
(a) Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by
$\theta(t)=\tan ^{-1}\left(\frac{v_{0 y}-\mathrm{g} t}{v_{0 x}}\right)$
(b) Show that the projection angle $\theta_{0}$ for a projectile launched from the origin is given by
$\theta_{0}=\tan ^{-1}\left(\frac{4 h_{m}}{R}\right)$
Where the symbols have their usual meaning.
(a) Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by
$\theta(t)=\tan ^{-1}\left(\frac{v_{0 y}-\mathrm{g} t}{v_{0 x}}\right)$
(b) Show that the projection angle $\theta_{0}$ for a projectile launched from the origin is given by
$\theta_{0}=\tan ^{-1}\left(\frac{4 h_{m}}{R}\right)$
Where the symbols have their usual meaning.
solution:
(a) Let $v_{0 x}$ and $v_{0 y}$ respectively be the initial components of the velocity of the projectile along horizontal $(x)$ and vertical $(y)$ directions.
Let $v_{x}$ and $v_{y}$ respectively be the horizontal and vertical components of velocity at a point $\mathrm{P}$.
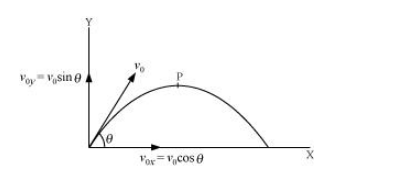
Time taken by the projectile to reach point P = t
Applying the first equation of motion along the vertical and horizontal directions, we get:
$v_{y}=v_{0 y}=\mathrm{g} t$
And $v_{x}=v_{0 x}$
$\therefore \tan \theta=\frac{v_{y}}{v_{x}}=\frac{v_{0 y}-\mathrm{g} t}{v_{0 x}}$
$\theta=\tan ^{-1}\left(\frac{v_{0 y}-\mathrm{g} t}{v_{0 x}}\right)$
(b) Maximum vertical height, $h_{m}=\frac{u_{0}^{2} \sin ^{2} \theta}{2 g} \quad \ldots(i)$
Horizontal range, $R=\frac{u_{0}^{2} \sin 2 \theta}{g} \quad \ldots(i i)$
Solving equations (i) and (ii), we get:
$\frac{h_{m}}{R}=\frac{\sin ^{2} \theta}{2 \sin 2 \theta}=\frac{\sin ^{2} \theta}{4 \sin \theta \cos \theta}=\frac{\sin \theta}{4 \cos \theta}$
$\Rightarrow \frac{h_{m}}{R}=\frac{\operatorname{Tan} \theta}{4}$
$\Rightarrow \theta=\operatorname{Tan}^{-1}\left(\frac{4 h_{m}}{R}\right)$
(a) Let $v_{0 x}$ and $v_{0 y}$ respectively be the initial components of the velocity of the projectile along horizontal $(x)$ and vertical $(y)$ directions.
Let $v_{x}$ and $v_{y}$ respectively be the horizontal and vertical components of velocity at a point $\mathrm{P}$.
Time taken by the projectile to reach point P = t
Applying the first equation of motion along the vertical and horizontal directions, we get:
$v_{y}=v_{0 y}=\mathrm{g} t$
And $v_{x}=v_{0 x}$
$\therefore \tan \theta=\frac{v_{y}}{v_{x}}=\frac{v_{0 y}-\mathrm{g} t}{v_{0 x}}$
$\theta=\tan ^{-1}\left(\frac{v_{0 y}-\mathrm{g} t}{v_{0 x}}\right)$
(b) Maximum vertical height, $h_{m}=\frac{u_{0}^{2} \sin ^{2} \theta}{2 g} \quad \ldots(i)$
Horizontal range, $R=\frac{u_{0}^{2} \sin 2 \theta}{g} \quad \ldots(i i)$
Solving equations (i) and (ii), we get:
$\frac{h_{m}}{R}=\frac{\sin ^{2} \theta}{2 \sin 2 \theta}=\frac{\sin ^{2} \theta}{4 \sin \theta \cos \theta}=\frac{\sin \theta}{4 \cos \theta}$
$\Rightarrow \frac{h_{m}}{R}=\frac{\operatorname{Tan} \theta}{4}$
$\Rightarrow \theta=\operatorname{Tan}^{-1}\left(\frac{4 h_{m}}{R}\right)$