A side of an equilateral triangle is 24 cm long. A second equilateral triangle is inscribed in it by joining the midpoints of the sides of the first triangle; the process is continued. Find the perimeter of the sixth inscribed equilateral triangle.
To Find: The perimeter of the sixth inscribed equilateral triangle.
1st Given: Side of an equilateral triangle is $24 \mathrm{~cm}$ long.
As 2nd triangle is formed by joining the midpoints of the sides of the first triangle whose side is equal to 24cm
$2^{n}$ [As shown in the figure]
So Side of a 2nd equilateral triangle is 12 cm long [half of the first triangle side]
$\therefore$ Side of $2^{\text {nd }}$ equilateral triangle $=$ half of side of a $1^{\text {st }}$ equilateral triangle
$\therefore$ Side of $3^{\text {rd }}$ equilateral triangle $=$ half of side of a $2^{\text {nd }}$ equilateral triangle
$\therefore$ and So on
Therefore, Side of $6^{\text {th }}$ equilateral triangle $=$ half of side of a $5^{\text {th }}$ equilateral triangle
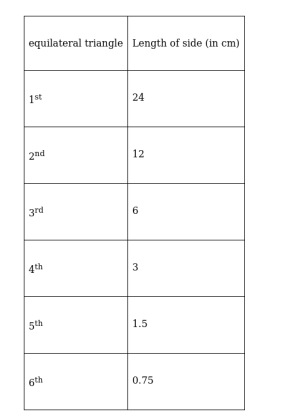
So, Perimeter of a 6th equilateral triangle is 3 times the side of a 6th equilateral triangle
[NOTE: Perimeter of the triangle is equal to the sum of all three sides of the triangle, and in case of an equilateral triangle all sides are equal]
So, Perimeter of $6^{\text {th }}$ equilateral triangle $=3 \times 0.75=2.25 \mathrm{~cm}$