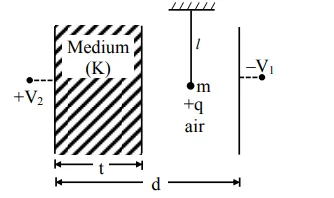
A simple pendulum of mass 'm', length 'l' and charge '+q' suspended in the electric field produced by two conducting parallel plates as shown. The value of deflection of pendulum in equilibrium position will be
Correct Option: , 3
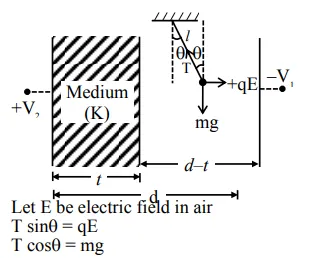
$\tan \theta=\frac{\mathrm{qE}}{\mathrm{mg}}$
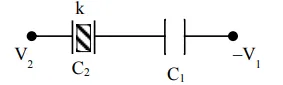
$\mathrm{Q}=\left[\frac{\mathrm{C}_{1} \mathrm{C}_{2}}{\mathrm{C}_{1}+\mathrm{C}_{2}}\right]\left[\mathrm{V}_{1}+\mathrm{V}_{2}\right]$
$\mathrm{E}=\frac{\mathrm{Q}}{\mathrm{A} \in_{\mathrm{o}}}=\left[\frac{\mathrm{C}_{1} \mathrm{C}_{2}}{\mathrm{C}_{1}+\mathrm{C}_{2}}\right] \frac{\left[\mathrm{V}_{1}+\mathrm{V}_{2}\right]}{\mathrm{A} \in_{\mathrm{o}}}$
$\mathrm{C}_{1}=\frac{\in_{\mathrm{o}} \mathrm{A}}{\mathrm{d}-\mathrm{t}} \Rightarrow \mathrm{E}=\frac{\mathrm{C}_{2}\left[\mathrm{~V}_{1}+\mathrm{V}_{2}\right]}{\left(\mathrm{C}_{1}+\mathrm{C}_{2}\right)(\mathrm{d}-\mathrm{t})}$
Now $\theta=\tan ^{-1}\left[\frac{\mathrm{q} . \mathrm{E}}{\mathrm{mg}}\right]$
$\theta=\tan ^{-1}\left[\frac{\mathrm{q}}{\mathrm{mg}} \times \frac{\mathrm{C}_{2}\left(\mathrm{~V}_{1}+\mathrm{V}_{2}\right)}{\left(\mathrm{C}_{1}+\mathrm{C}_{2}\right)(\mathrm{d}-\mathrm{t})}\right]$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.