Question:
A small ball of mass $m$ is thrown upward with velocity $u$ from the ground. The ball experiences a resistive force $m k v^{2}$ where $v$ is its speed. The maximum height attained by the ball is :
Correct Option: , 4
Solution:
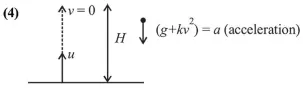
$\vec{F}=m k v^{2}-m g$ $\left(\because m g\right.$ and $m k v^{2}$ act opposite to each other)
$\vec{a}=\frac{\vec{F}}{m}=-\left[k v^{2}+g\right]$
$\Rightarrow v \cdot \frac{d v}{d h}=-\left[k v^{2}+g\right]$ $\left(\because a=v \frac{d v}{d h}\right)$
$\Rightarrow \int_{u}^{0} \frac{v \cdot d v}{k v^{2}+g}=\int_{0}^{h} d h$
$\Rightarrow \frac{1}{2 k} \ln \left[k v^{2}+g\right]_{u}^{0}=-h$
$\Rightarrow \frac{1}{2 k} \ln \left[\frac{k u^{2}+g}{g}\right]=h$
