A solid cone of base radius 10 cm is cut into two parts through the midpoint of its height, by a plane parallel to its base.

Solution:

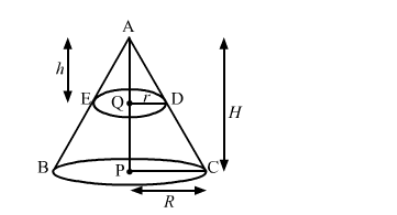
We have,

Radius of solid cone, $R=\mathrm{CP}=10 \mathrm{~cm}$,

Let the height of the solid cone be, $\mathrm{AP}=H$,

the radius of the smaller cone, $\mathrm{QD}=r$ and

the height of the smaller cone be, $\mathrm{AQ}=h$.

Also, $\mathrm{AQ}=\frac{\mathrm{AP}}{2}$ i. e. $h=\frac{H}{2}$ or $H=2 h$  .........(i)

Now, in $\Delta \mathrm{AQD}$ and $\triangle \mathrm{APC}$,

$\angle \mathrm{QAD}=\angle \mathrm{PAC} \quad($ Common angle $)$

$\angle \mathrm{AQD}=\angle \mathrm{APC}=90^{\circ}$

So, by AA criteria

$\triangle \mathrm{AQD} \sim \mathrm{APC}$

$\Rightarrow \frac{\mathrm{AQ}}{\mathrm{AP}}=\frac{\mathrm{QD}}{\mathrm{PC}}$

$\Rightarrow \frac{h}{H}=\frac{r}{R}$

$\Rightarrow \frac{h}{2 h}=\frac{r}{R} \quad[\mathrm{Using}(\mathrm{i})]$

$\Rightarrow \frac{1}{2}=\frac{r}{R}$

$\Rightarrow R=2 r \quad \ldots$ (ii)

As,

Volume of smaller cone $=\frac{1}{3} \pi r^{2} h$

And,

Volume of solid cone $=\frac{1}{3} \pi R^{2} H$

$=\frac{1}{3} \pi(2 r)^{2} \times(2 h) \quad[$ Using (i) and (ii) $]$

$=\frac{8}{3} \pi r^{2} h$

So,

Volume of frustum $=$ Volume of solid cone $-$ Volume of smaller cone

$=\frac{8}{3} \pi r^{2} h-\frac{1}{3} \pi r^{2} h$

$=\frac{7}{3} \pi r^{2} h$

Now, the ratio of the volumes of the two parts $=\frac{\text { Volume of the smaller cone }}{\text { Volume of the frustum }}$

$=\frac{\left(\frac{1}{3} \pi r^{2} h\right)}{\left(\frac{7}{3} \pi r^{2} h\right)}$

$=\frac{1}{7}$

$=1: 7$

So, the ratio of the volume of the two parts of the cone is 1 : 7.