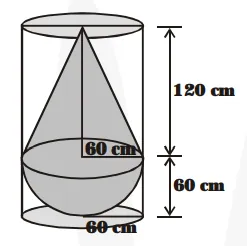
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom.

Height of the conical part = 120 cm

Base radius of the conical part = 60 cm

$\therefore$ Volume of the conical part $=\frac{\mathbf{1}}{\mathbf{3}} \pi \mathrm{r}^{2} \mathrm{~h}$

$=\frac{\mathbf{1}}{\mathbf{3}} \times \frac{\mathbf{2 2}}{\mathbf{7}} \times 60^{2} \times 120 \mathrm{~cm}^{3}$

Radius of the hemispherical part = 60 cm.

$\therefore$ Volume of the hemispherical part $=\frac{\mathbf{2}}{\mathbf{3}} \pi \mathrm{r}^{3}$

$=\frac{2}{3} \times \frac{22}{7} \times(60)^{3} \mathrm{~cm}^{3}$

$\therefore$ Volume of the solid $=$ [Volume of conical part] $+$ [Volume of hemispherical part]

$=\left[\frac{1}{3} \times \frac{22}{7} \times 60^{2} \times 120\right]+\left[\frac{2}{3} \times \frac{22}{7} \times 60^{3}\right] \mathrm{cm}^{3}$

$=\frac{\mathbf{2}}{\mathbf{3}} \times \frac{\mathbf{2 2}}{\mathbf{7}} \times 60^{2}[60+60] \mathrm{cm}^{3}$

$=\frac{2}{3} \times \frac{22}{7} \times 60 \times 60 \times 120 \mathrm{~cm}^{3}=\frac{6336000}{7} \mathrm{~cm}^{3}$

$\Rightarrow$ Volume of water in the cylinder $=\pi \mathrm{r}^{2} \mathrm{~h}$

$=\frac{\mathbf{2 2}}{\mathbf{7}} \times 60 \times 60 \times 180$

$=\frac{14256000}{7} \mathrm{~cm}^{3}$

$\therefore$ Volume of water left in the cylinder

$=\left[\frac{14256000}{7}-\frac{6336000}{7}\right] \mathrm{cm}^{3}$

$=\frac{7920000}{7} \mathrm{~cm}^{3}$

$=1131428.57142 \mathrm{~cm}^{3}=\frac{\mathbf{1 1 3 1 4 2 8 . 5 7 1 4 2}}{\mathbf{1 0 0 0 0 0 0}} \mathrm{m}^{3}$

$=1.13142857142 \mathrm{~m}^{3}=1.131 \mathrm{~m}^{3}$ (approx).