A solid cylinder rolls up an inclined plane of angle of inclination 30°.

A solid cylinder rolling up an inclination is shown in the following figure.

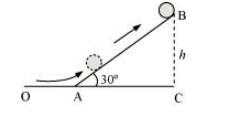
Initial velocity of the solid cylinder, v = 5 m/s

Angle of inclination, $\theta=30^{\circ}$

Height reached by the cylinder $=h$

(a) Energy of the cylinder at point A:

$\mathrm{KE}_{\mathrm{rm}}=\mathrm{KE}_{\text {tans }}$

$\frac{1}{2} I \omega^{2}=\frac{1}{2} m v^{2}$

Energy of the cylinder at point $\mathrm{B}=m \mathrm{~g} h$

Using the law of conservation of energy, we can write:

$\frac{1}{2} I \omega^{2}=\frac{1}{2} m v^{2}=m \mathrm{~g} h$

Moment of inertia of the solid cylinder, $I=\frac{1}{2} m r^{2}$

$\therefore \frac{1}{2}\left(\frac{1}{2} m r^{2}\right) \omega^{2}+\frac{1}{2} m v^{2}=m \mathrm{~g} h$

$\frac{1}{4} m r^{2} \omega^{2}+\frac{1}{2} m v^{2}=m g h$

But we have the relation, $v=r \omega$

$\therefore \frac{1}{4} v^{2}+\frac{1}{2} v^{2}=\mathrm{gh}$

$\frac{3}{4} v^{2}=\mathrm{g} h$

$\therefore h=\frac{3}{4} \frac{v^{2}}{g}$

$\therefore h=\frac{3 v^{2}}{4} \frac{v}{g}$

$=\frac{3}{4} \times \frac{5 \times 5}{9.8}=1.91 \mathrm{~m}$

In $\triangle A B C$ :

$\sin \theta=\frac{\mathrm{BC}}{\mathrm{AB}}$

$\sin 30^{\circ}=\frac{h}{\mathrm{AB}}$

$\mathrm{AB}=\frac{1.91}{0.5}=3.82 \mathrm{~m}$

Hence, the cylinder will travel 3.82 m up the inclined plane.

(b) For radius of gyration K, the velocity of the cylinder at the instance when it rolls back to the bottom is given by the relation:

$v=\left(\frac{2 \mathrm{~g} h}{1+\frac{K^{2}}{R^{2}}}\right)^{\frac{1}{2}}$

$\therefore v=\left(\frac{2 \mathrm{~g} \mathrm{AB} \sin \theta}{1+\frac{K^{2}}{R^{2}}}\right)^{\frac{1}{2}}$

For the solid cylinder, $K^{2}=\frac{R^{2}}{2}$

$\therefore v=\left(\frac{2 \mathrm{~g} \mathrm{AB} \sin \theta}{1+\frac{1}{2}}\right)^{\frac{1}{2}}$

$=\left(\frac{4}{3} \mathrm{~g} \mathrm{AB} \sin \theta\right)^{\frac{1}{2}}$

The time taken to return to the bottom is:

$t=\frac{\mathrm{AB}}{v}$

$=\frac{A B}{\left(\frac{4}{3} g A B \sin \theta\right)^{\frac{1}{2}}}=\left(\frac{3 A B}{4 g \sin \theta}\right)^{\frac{1}{2}}$

$=\left(\frac{11.46}{19.6}\right)^{\frac{1}{2}}=0.764 \mathrm{~s}$

Therefore, the total time taken by the cylinder to return to the bottom is (2 × 0.764) 1.53 s.