A solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is 2.1 cm and the height of the cone is 4 cm. The solid is placed in a cylindrical tub full of water in such a way that the whole solid is submerged in water. If the radius of the cylinder is 5 cm and its height is 9.8 cm, find the volume of the water left in the tub.
The object is shown in the figure below.
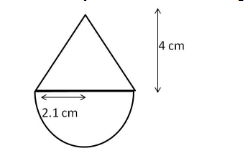
Radius of hemisphere = 2.1 cm
Volume of hemisphere $=\frac{2}{3} \pi r^{3}=\frac{2}{3} \times \frac{22}{7} \times 2.1 \times 2.1 \times 2.1=19.404 \mathrm{~cm}^{3}$
Height of cone = 4 cm
Volume of cone $=\frac{1}{3} \pi r^{2} \mathrm{~h}=\frac{1}{3} \times \frac{22}{7} \times 2.1 \times 2.1 \times 4=18.48 \mathrm{~cm}^{3}$
Volume of the object $=18.48+19.404=37.884 \mathrm{~cm}^{3}$
Volume of cylindrical tub $=\pi r^{2} \mathrm{~h}=\frac{22}{7} \times 5 \times 5 \times 9.8=770 \mathrm{~cm}^{3}$
When the object is immersed in the tub, volume of water equal to the volume of the object is displaced from the tub.
Volume of water left in the tub $=770-37.884=732.116 \mathrm{~cm}^{3}$