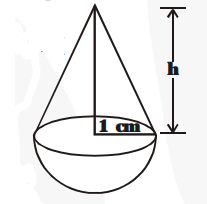
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius.

Here, r = 1 cm and h = 1 cm.

Volume of the conical part $=\frac{\mathbf{1}}{\mathbf{3}} \pi r^{2} h$

and volume of the hemispherical part $\frac{2}{3} \pi \mathrm{r}^{3}$

$\therefore$ Volume of the solid shape

$=\frac{1}{3} \pi r^{2} h+\frac{2}{3} \pi r^{3}=\frac{1}{3} \pi r^{2}[h+2 r]$

$=\frac{\mathbf{1}}{\mathbf{3}} \pi(1)^{2}[1+2(1)] \mathrm{cm}^{3}$

$=\frac{\mathbf{1}}{\mathbf{3}} \pi \times 1 \times 3 \mathrm{~cm}^{3}=\pi \mathrm{cm}^{3}$