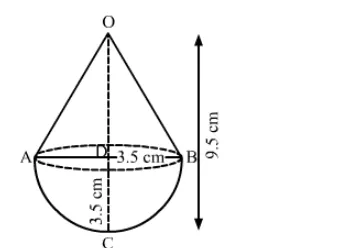
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them being 3.5 cm

We have,

Radius of cone $=$ Radius of hemisphere $=r=3.5 \mathrm{~cm}$ or $\mathrm{AD}=\mathrm{BD}=\mathrm{CD}=3.5 \mathrm{~cm}$,

Total height of the solid, $O C=9.5 \mathrm{~cm}$

$\Rightarrow \mathrm{OD}+\mathrm{CD}=9.5$

$\Rightarrow \mathrm{OD}+3.5=9.5$

$\Rightarrow \mathrm{OD}=6 \mathrm{~cm}$

$\Rightarrow$ Height of cone, $h=6 \mathrm{~cm}$

Now,

Volume of solid = Volume of cone + Volume of hemisphere

$=\frac{1}{3} \pi r^{2} h+\frac{2}{3} \pi r^{3}$

$=\frac{1}{3} \pi r^{2}(h+2 r)$

$=\frac{1}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times(6+2 \times 3.5)$

$=\frac{1}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times(6+7)$

$=\frac{1}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times 13$

$=\frac{500.5}{3}$

$\approx 166.83 \mathrm{~cm}^{3}$

So, the volume of the solid is 166.83 cm3.