A solid right circular cone of height 120 cm

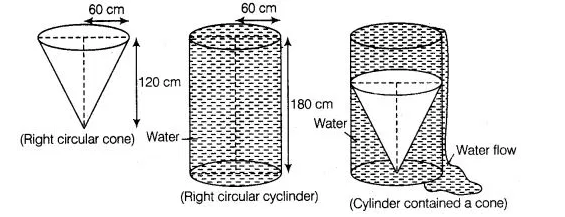
(i)   Whenever we placed a solid right circular cone in a right circular cylinder with full of water, then volume of a solid right circular cone is equal to

the volume of water failed from the cylinder.

(ii)  Total volume of water in a cylinder is equal to the volume of the cylinder.

(iii) Volume of water left in the cylinder = Volume of the right circular cylinder – volume of a

right circular cone.

Now, given that

Height of a right circular cone = 120 cm

Radius of a right circular cone = 60 cm

$\therefore$ Volume of a right circular cone $=\frac{1}{3} \pi r^{2} \times h$

$=\frac{1}{3} \times \frac{22}{7} \times 60 \times 60 \times 120$

$=\frac{22}{7} \times 20 \times 60 \times 120$

$=144000 \pi \mathrm{cm}^{3}$

$\therefore$ Volume of a right circular cone $=$ Volume of water falled from the cylinder

$=144000 \pi \mathrm{cm}^{3}$ [from point (i)]

Given that, height of a right circular cylinder $=180 \mathrm{~cm}$

and radius of a right circular cylinder $=$ Radius of a right circular cone

$=60 \mathrm{~cm}$

$\therefore$ Volume of a right circular cylinder $=\pi r^{2} \times h$

$=\pi \times 60 \times 60 \times 180$

$=648000 \pi \mathrm{cm}^{3}$

So, volume of a right circular cylinder $=$ Total volume of water in a cylinder

$=648000 \pi \mathrm{cm}^{3}$ [from point (ii)]

From point (iii),

Volume of water left in the cylinder

$=$ Total volume of water in a cylinder - Volume of water falled from

the cylinder when solid cone is placed in it

$=648000 \pi-144000 \pi$

$=504000 \pi=504000 \times \frac{22}{7}=1584000 \mathrm{~cm}^{3}$

$=\frac{1584000}{(10)^{6}} m^{3}=1.584 m^{3}$

Hence, the required volume of water left in the cylinder is $1.584 \mathrm{~m}^{3}$.