A solid sphere of radius $R$ carries a charge $Q+q$ distributed uniformaly over its volume. A very small point like piece of it of mass $m$ gets detached from the bottom of the sphere and falls down vertically under gravity. This piece carries charge $q$. If it acquires a speed $v$ when it has fallen through a vertical height $y$ (see figure), then : (assume the remaining portion to be spherical).
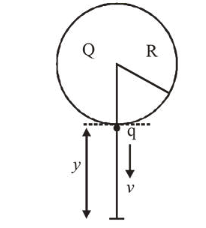
Correct Option: , 4
(4) By using energy conservation,
$\Delta K E+(\Delta P E)_{\text {Electro }}+(\Delta P E)_{\text {gravitational }}=0$
$\frac{1}{2} m V^{2}+\left(k \frac{Q q}{R+y}-k \frac{Q q}{R}\right)+(-m g y)=0$
$\Rightarrow \frac{1}{2} m V^{2}=m g y+k Q q\left(\frac{1}{R}-\frac{1}{R+y}\right)$
$\Rightarrow V^{2}=2 g y+\frac{2 k Q q}{m} \frac{y}{R(R+y)}$
or, $V^{2}=2 y\left[\frac{q Q}{4 \pi \varepsilon_{0} R(R+y) m}+g\right]$
