A solid sphere of radius 'r' is melted and recast into

Volume of sphere $=\frac{4}{3} \pi r^{3}$ ......(i)

Since,

The sphere is recast in to a hollow cylinder of uniform thickness 2 cm.

The external radius of hollow cylinder r1 = 4 cm

The internal radius of hollow cylinder $r_{2}=4-2=2 \mathrm{~cm}$

and height, h = 24 cm

Clearly,

The volume of hollow cylinder = volume of sphere

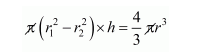
$\left(4^{2}-2^{2}\right) \times 24=\frac{4}{3} r^{3}$

$12 \times 24=\frac{4}{3} r^{3}$

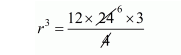
$r=\sqrt{12 \times 6 \times 3}$

$=\sqrt[3]{3 \times 2 \times 2 \times 2 \times 3 \times 3}$

$r=6 \mathrm{~cm}$