Question:
A source of light is placed in front of a screen. Intensity of light on the screen is I. Two Polaroids $P_{1}$ and $P_{2}$ are so placed in between the source of light and screen that the intensity of light on screen is $\mathrm{I} / 2 . \mathrm{P}_{2}$ should be rotated by an angle of (degrees) so that the intensity of light on the screen becomes $\frac{3 \mathrm{I}}{8}$.
Solution:
$I=\frac{I_{0}}{2} \cos ^{2} \phi$
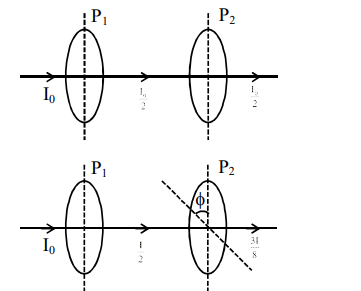
$\frac{I}{2} \cos ^{2} \phi=\frac{3 I}{8}$
$\cos ^{2} \phi=\frac{3}{4}$
$\cos ^{2} \phi=\frac{\sqrt{3}}{2}$
$\Rightarrow \phi=30$
Ans. 30
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
