A sphere of radius ' a ' and mass ' m ' rolls along

Question:

A sphere of radius ' $a$ ' and mass ' $m$ ' rolls along a horizontal plane with constant speed $v_{0}$. It encounters an inclined plane at angle $\theta$ and climbs upward. Assuming that it rolls without slipping, how far up the sphere will travel ?

  1. $\frac{10 v_{0}^{2}}{7 g \sin \theta}$

  2.  $\frac{v_{0}^{2}}{5 g \sin \theta}$

  3. $\frac{2}{5} \frac{v_{0}^{2}}{g \sin \theta}$

  4. $\frac{v_{0}^{2}}{2 g \sin \theta}$

Correct Option: 1

Solution:

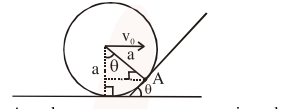
Angular momentum conservation about A

$\mathrm{mv}_{0} \mathrm{a} \cos \theta+\frac{2}{5} \mathrm{ma}^{2} \omega$

$=m v a+\frac{2}{5} m a^{2} \omega^{1}$

$\mathrm{mv}_{0} \mathrm{a}\left[\frac{2}{5}+\cos \theta\right]=\frac{7}{5} \mathrm{mva}$

$\mathrm{v}=\frac{5}{7}=\mathrm{v}_{0}\left[\frac{2}{5}+\cos \theta\right]$

$\frac{1}{2} \mathrm{mv}^{2}+\frac{1}{2} \mathrm{I} \omega^{2}=\frac{7}{10} \mathrm{mv}^{2}=\mathrm{mgh}$

No option Maching

Leave a comment

Comments

Ritil
May 26, 2022, 2:56 p.m.
I don't know why is everyone doing mistakes. At half of the places, they have directly conserved mechanical energy which is wrong since impulsive normal and friction force acts on colliding with the incline which reduces mechanical energy. The methodology shown in this is correct but there is some unknown random error unreasonable just to match the answer. And everyone is copying the random error
Close

Click here to get exam-ready with eSaral

For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.

Download Now

eSaral Gurukul

NEET

JEE Main

JEE Advanced

Our Telegram Channel

All Study Material