A sphere of radius 'a' and mass 'm' rolls along horizontal plane with constant speed $u_{-} 0$. It encounters an inclined plane at angle $\theta$ and climbs upward. Assuming that it rolls without slipping how far up the sphere will travel?
Note: NTA has dropped this question in the final official answer key.
Correct Option: , 2
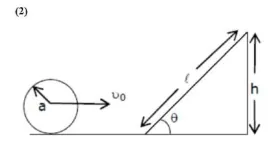
From energy conservation
$\mathrm{mgh}=\frac{1}{2} \mathrm{mv}_{0}^{2}+\frac{1}{2} \mathrm{I} \omega^{2}$
$\mathrm{mgh}=\frac{1}{2} \mathrm{mv}_{0}^{2}+\frac{1}{2} \times \frac{2}{5} \mathrm{ma}^{2} \times \frac{\mathrm{v}_{0}{ }^{2}}{\mathrm{~s}^{2}}$
$g h=\frac{1}{2} v_{0}^{2}+\frac{1}{5} v_{0}^{2}$
$g h=\frac{7}{10} v_{0}^{2}$
$h=\frac{7}{10} \frac{v_{0}^{2}}{g}$
from triangle, $\sin \theta=\frac{\mathrm{h}}{\ell}$
then $\mathrm{h}=\ell \sin \theta$
$\ell \sin \theta=\frac{7}{10} \frac{v_{0}^{2}}{9}$
$\ell=\frac{7}{10} \frac{v_{0}^{2}}{g \sin \theta}$
