A spherical glass vessel has a cylindrical neck $8 \mathrm{~cm}$ long, $2 \mathrm{~cm}$ in diameter; the diamter of the spherical part is $8.5 \mathrm{~cm}$. By measuring the amount of water it holds, a child finds its volume to be $345 \mathrm{~cm}^{3}$. Check whether she is correct, taking the above as the inside measurements, and $\pi$ $=3.14$.
The cylinder neck has length = 8 cm
and radius = 1 cm
Volume of the cylinder part
$=\pi(1)^{2} \times 8 \mathrm{~cm}^{3}$
$=8 \pi \mathrm{cm}^{3}$
The radius of the spherical part
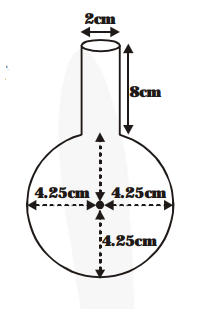
$=\frac{85}{2} \mathrm{~cm}=4.25 \mathrm{~cm}$
Volume of the spherical part
$=\frac{\mathbf{4}}{\mathbf{3}} \pi \times(4.25)^{3}$
Total volume of water
$=8 \pi+\frac{\mathbf{4}}{\mathbf{3}} \times(4.25)^{3} \pi \mathrm{cm}^{3}$
$=8 \times 3.14+\frac{\mathbf{4}}{\mathbf{3}} \times 3.14 \times(4.25)^{3} \mathrm{~cm}^{3}$
$=25.12+321.38$ (approx.)
$=346.5 \mathrm{~cm}^{3}$ (approx.)
So, $345 \mathrm{~cm}^{3}$ is not correct.