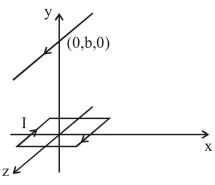
A square loop of side $2 \mathrm{a}$ and carrying current I is kept in xz plane with its centre at origin. A long wire carrying the same current $\mathrm{I}$ is placed parallel to z-axis and passing through point $(0, b, 0),(b>>a)$. The magnitude of torque on the loop about z-ax is will be :
Correct Option: 1
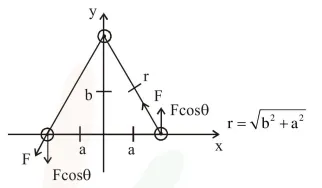
$\mathrm{F}=\mathrm{BI} 2 \mathrm{a}=\frac{\mu_{0} \mathrm{I}}{2 \pi \mathrm{r}} \mathrm{I} \times 2 \mathrm{a}$
$\mathrm{F}=\frac{\mu_{0} \mathrm{I}^{2} \mathrm{a}}{\pi \sqrt{\mathrm{b}^{2}+\mathrm{a}^{2}}}$
$\tau=\mathrm{F} \cos \theta \times 2 \mathrm{a}$
$=\frac{\mu_{0} I^{2} a}{\pi \sqrt{b^{2}+a^{2}}} \times \frac{b}{\sqrt{b^{2}+a^{2}}} \times 2 a$
$\tau=\frac{2 \mu_{0} I^{2} a^{2} b}{\pi\left(a^{2}+b^{2}\right)}$
If $b>a$ then $\tau=\frac{2 \mu_{0} I^{2} a^{2}}{\pi b}$
But among the given options (1) is most appropriate
