A straight highway leads to the foot of a tower.

Let PQ = h metres be the height of the tower. P is the top of the tower. PX is horizontal line through P. The first and second positions of the car are at A and B respectively.

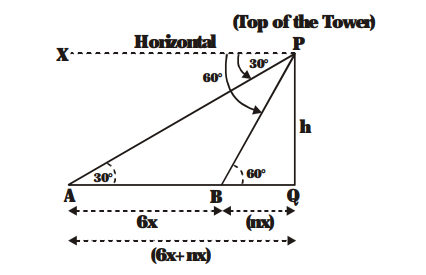
$\angle \mathrm{APX}=30^{\circ}$

(Angle of depression of the car when observed at $\mathrm{A}$ )

and $\angle \mathrm{BPX}=60^{\circ}$

(Angle of depression of the car when observed at B)

Then $\angle \mathrm{PAQ}=30^{\circ}$ and $\angle \mathrm{PBQ}=60^{\circ}$

Let the speed of the car be x m/second

Then distance AB = 6 x metres.

Let the time taken from B to Q be n second.

Then distance BQ = nx metres.

In right $\triangle \mathrm{PAQ}$,

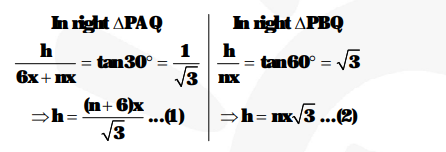
From (1) and (2), we have

$\frac{(m+6) x}{\sqrt{3}}=m x \sqrt{3}$

$\Rightarrow \mathrm{n}+6=\mathrm{m} \sqrt{\mathbf{3}} \times \sqrt{\mathbf{3}}$

$\Rightarrow 3 n=n+6$

$\Rightarrow 2 n=6$

$\Rightarrow \mathrm{n}=3$

Hence, the time from B to $Q=3$ seconds.