A street light bulb is fixed on a pole 6 m

Let A be the position of the street bulb fixed on a pole AB = 6 m and CD = 1.5 m be the height of a woman and her shadow be ED = 3 m. Let

distance between pole and woman be x m.

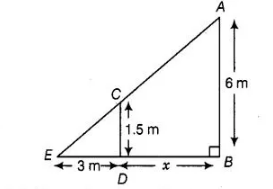
Here, woman and pole both are standing vertically.

So, $C D \| A B$

In $\triangle C D E$ and $\triangle A B E, \quad \angle E=\angle E \quad$ [common angle]

$\angle A B E=\angle C D E$ [each equal to $90^{\circ}$ ]

$\begin{array}{lll}\therefore & \Delta C D E \sim \Delta A B E & \text { [by AAA similarity criterion] }\end{array}$

Then, $\frac{E D}{E B}=\frac{C D}{A B}$

$\Rightarrow$ $\frac{3}{3+x}=\frac{1.5}{6}$

$\Rightarrow \quad 3 \times 6=1.5(3+x)$

$\Rightarrow \quad 18=1.5 \times 3+1.5 x$

$\Rightarrow \quad 1.5 x=18-4.5$

$\therefore$ $x=\frac{13.5}{1.5}=9 \mathrm{~m}$

Hence, she is at the distance of 9 m from the base of the pole.