Question:
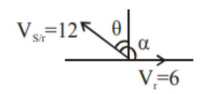
A swimmer can swim with velocity of $12 \mathrm{~km} / \mathrm{h}$ in still water. Water flowing in a river has velocity $6 \mathrm{~km} / \mathrm{h}$. The direction with respect to the direction of flow of river water he should swim in order to reach the point on the other bank just opposite to his starting point is - (Round off to the Nearest Integer) (find the angle in degree)
Solution:
(120)
$12 \sin \theta=v_{r}$
$\sin \theta=\frac{1}{2}$
$\theta=30^{\circ}$
$\therefore \quad \alpha=120^{\circ}$
