A tangent PQ at a point P of a circle of radius

O is the centre of the circle. The radius of the circle is 5 cm.

PQ is tangent to the circle at P. Then

$\mathrm{OP}=5 \mathrm{~cm}$ and $\angle \mathrm{OPQ}=90^{\circ}$

We are given that $\mathrm{OQ}=12 \mathrm{~cm}$.

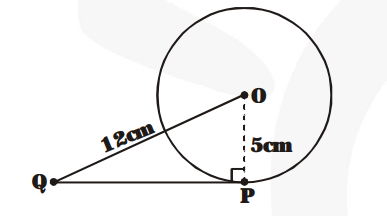
By Pythagoras Theorem, we have

$\mathrm{PQ}^{2}=\mathrm{OQ}^{2}-\mathrm{OP}^{2}$

$=(12)^{2}-(5)^{2}=144-25=119$

$\Rightarrow \mathrm{PQ}=\sqrt{\mathbf{1 1 9}} \mathrm{cm}$

Hence, the correction option is (D).