A tent is in the shape of a cylinder surmounted by a conical top.

Radius of the cylindrical base = 2m and

height = 2.1 m. The curved surface area of the cylindrical part

$=2 \pi \times(2) \times(2.1) \mathrm{m}^{2}$ (i.e., $2 \pi \mathrm{rh}$ )

$=4 \times \frac{\mathbf{2 2}}{\mathbf{7}} \times 2.1 \mathrm{~m}^{2}$

$=26.4 \mathrm{~m}^{2}$

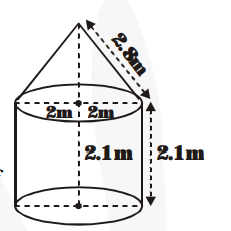
Now, for the conical part, we have r = 2m and

$\ell$ (slant height) $=2.8 \mathrm{~m}$The curved surface area of the conical part $=\pi \mathrm{r} \ell$ 

$=\frac{\mathbf{2 2}}{\mathbf{7}} \times 2 \times 2.8 \mathrm{~m}^{2}$

$=17.6 \mathrm{~m}^{2}$

Then the area of the canvas

$=26.4 \mathrm{~m}^{2}+17.6 \mathrm{~m}^{2}=44 \mathrm{~m}^{2}$

Total cost of the canvas at the rate of Rs. 500 per $\mathrm{m}^{2}$

= Rs. 500 × 44 = Rs. 22000