A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it.

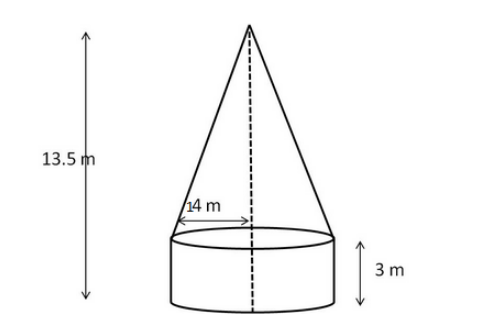
Radius of the cylinder = 14 m
Radius of the base of the cone = 14 m
Height of the cylinder (h) = 3 m
Total height of the tent = 13.5 m

Surface area of the cylinder $=2 \pi r h=\left(2 \times \frac{22}{7} \times 14 \times 3\right) \mathrm{m}^{2}=264 \mathrm{~m}^{2}$

Height of the cone $=$ Total height $-$ Height of cone $=(13.5-3) \mathrm{m}=10.5 \mathrm{~m}$

Surface area of the cone $=\pi r \sqrt{r^{2}+h^{2}}$

$=\pi r \sqrt{r^{2}+h^{2}}=\left(\frac{22}{7} \times 14 \times \sqrt{14^{2}+10.5^{2}}\right) \mathrm{m}^{2}$

$=(44 \times \sqrt{196+110.25}) \mathrm{m}^{2}=(44 \times \sqrt{306.25}) \mathrm{m}^{2}$

$=(44 \times 17.5) \mathrm{m}^{2}=770 \mathrm{~m}^{2}$

Total surface area $=(264+770) \mathrm{m}^{2}=1034 \mathrm{~m}^{2}$

$\therefore$ Cost of cloth $=$ Rs $1034 \times 80=$ Rs 82720