A tent of height 77 dm is in the form of a right circular

Given:

Height of the tent $\mathrm{h}=77 \mathrm{dm}=7.7 \mathrm{~m}$, diameter of cylinder $d=36 \mathrm{~m}$

Height of the cylinder h1 = 44 dm = 4.4 m, height of cone h2 = 33 dm = 3.3 m

We have the following diagram

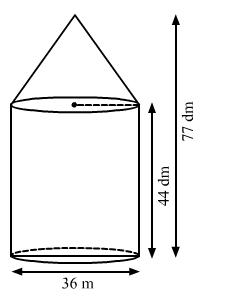
Radius $r=\frac{d}{2}=\frac{36}{2}=18 \mathrm{~m}$

The curved area $S_{1}$ of cylinder is given by

$S_{1}=2 \pi \mathrm{rh}=2 \times \frac{22}{7} \times 18 \times 4.4$

$=497.82 \mathrm{~m}^{2}$

The slant height of the cone is

$l=\sqrt{h^{2}+r^{2}}$

$=\sqrt{3 \cdot 3^{2}+18^{2}}$

$=\sqrt{334.89}$

$=18.3 \mathrm{~m}$

The curved area of the cone is given by

$S_{2}=\pi \mathrm{rl}=\frac{22}{7} \times 18 \times 18.3$

$=1035.25 \mathrm{~m}^{2}$

The total area of the canvas required is given as

S = S1 + S2

= 497.82 + 1035.25

=1533.07 m2

Therefore the cost of the canvas at the rate of Rs 3.5 per square meter is given by

$1533.07 \times 3.5$

$=R s 5365.745$

Hence the cost of the canvas is Rs 5365.745