A thin rod of mass $0.9 \mathrm{~kg}$ and length $1 \mathrm{~m}$ is suspended, at rest, from one end so that it can freely oscillate in the vertical plane. A particle of move $0.1 \mathrm{~kg}$ moving in a straight line with velocity $80 \mathrm{~m} / \mathrm{s}$ hits the rod at its bottom most point and sticks to it (see figure). The angular speed (in $\mathrm{rad} / \mathrm{s}$ ) of the rod immediately after the collision will be _____
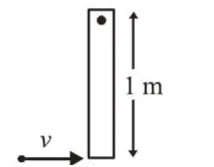
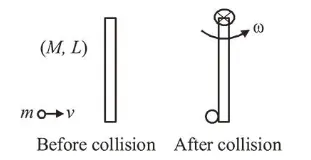
Using principal of conservation of angular momentum we have
$\vec{L}_{i}=\vec{L}_{f} \Rightarrow m v L=I \omega$
$\Rightarrow m v L=\left(\frac{M L^{2}}{3}+m L^{2}\right) \omega$
$\Rightarrow 0.1 \times 80 \times 1=\left(\frac{0.9 \times 1^{2}}{3}+0.1 \times 1^{2}\right) \omega$
$\Rightarrow 8=\left(\frac{3}{10}+\frac{1}{10}\right) \omega \Rightarrow 8=\frac{4}{10} \omega$
$\Rightarrow \omega=20 \mathrm{rad} / \mathrm{sec}$
