Question:
A town B is 12 km south and 18 km west of a town A. Show that the bearing of $B$ from $A$ is $S 56^{\circ} 20^{\prime} W .$ Also, find the distance of $B$ from $A .$
Solution:
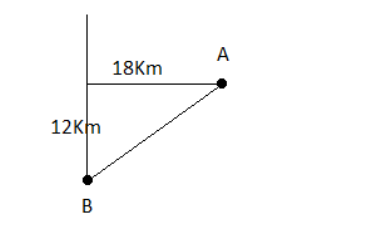
Distance from $A$ to $B$ is $=\sqrt{12^{2}+18^{2}}=\sqrt{468}=21.63 \mathrm{Km}$
Let, bearing from $A$ to $B$ is $\theta$.
So, $\tan \theta=\frac{18}{12}=\frac{3}{2}$
$\theta=\tan ^{-1}\left(\frac{3}{2}\right)=56.31^{\circ}=56^{\circ} 20^{\prime}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
