A train covered a certain distance at a uniform speed. If the train could have been 10 km/hr. faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/hr; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Let the actual speed of the train be Xkm\h mathrm{~km} / \mathrm{hr}$ and the actual time taken by y hours. Then,
Dis $\tan c e=$ Speed $\times$ Time
Distance covered $=(x y) \mathrm{km} \cdots(i)$
If the speed is increased by $10 \mathrm{Km} / \mathrm{hr}$, then time of journey is reduced by 2 hours
when speed is $(x+10) \mathrm{km} / h r$, time of journey is $(y-2)$ hours
- Distance covered $=(x+10)(y-2)$
$x y=(x+10)(y-2)$
$x y=x y+10 y-2 x-20$
$-2 x+10 y-20=0$
$-2 x+3 y-12=0$....(iii)
When the speed is reduced by $10 \mathrm{Km} / \mathrm{hr}$, then the time of journey is increased by 3 hours when speed is $(x-10) \mathrm{Km} / \mathrm{hr}$, time of journey is $(y+3)$ hours
$=$ Distance covered $=(x-10)(y+3)$
$x y=(x-10)(y+3)$
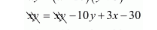
$0=-10 y+3 x-30$
$3 x-10 y-30=0 \cdots(iii)$
Thus, we obtain the following system of equations:
$-x+5 y-10=0$
$3 x-10 y-30=0$
By using cross multiplication, we have
$\frac{x}{5 x-30-(-10) \times-10}=\frac{-y}{(-1 \times-30)-(3 x-10)}=\frac{1}{(-1 \times-10)-(3 \times 5)}$
$\frac{x}{-150-100}=\frac{-y}{30+30}=\frac{1}{10-15}$
$\frac{x}{-250}=\frac{-y}{60}=\frac{1}{-5}$
$x=\frac{-250}{-5}$
$x=50$
$y=\frac{-60}{-5}$
$y=12$
Putting the values of x and y in equation (i), we obtain
Distance $=x y \mathrm{~km}$
$=50 \times 12$
$=600 \mathrm{~km}$
Hence, the length of the journey is $600 \mathrm{~km}$