A TV tower stands vertically on a bank of a canal.

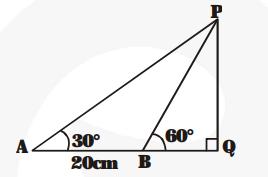
Let $P Q=h$ metres be the height of the tower and $B Q=x$ metres be the width of the canal $\angle \mathrm{PBQ}=60^{\circ}$

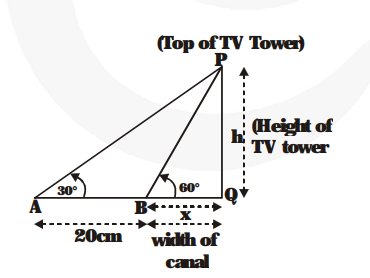
Now, the angle of elevation of the top of the tower from the point A = 30°,

i.e., $\angle \mathrm{PAQ}=30^{\circ}$ where $\mathrm{AB}=20$ metres

From $\triangle \mathrm{PBQ}$,

$\frac{h}{x}=\tan 60^{\circ}$

$\Rightarrow \frac{\mathbf{h}}{\mathbf{x}}=\sqrt{\mathbf{3}}$ or $\mathrm{h}=x \sqrt{\mathbf{3}}$  ...(1)

From $\triangle \mathrm{PAQ}$,

$\frac{\mathbf{h}}{\mathbf{2 0}+\mathbf{x}}=\tan 30^{\circ}$

$\frac{1}{\sqrt{3}}$

$h=\frac{20+x}{\sqrt{3}}$ ...(2)

From (1) and (2), we have $\mathbf{x} \sqrt{\mathbf{3}}=\frac{\mathbf{2 0}+\mathbf{x}}{\sqrt{\mathbf{3}}}$

$\Rightarrow 3 x=20+x$ or $2 x=20 \Rightarrow x=10$

From $(1), h=10 \sqrt{3} \mathrm{~m}$