A two-digit number is 3 more than 4 times the sum of its digits.

Let the tens place digit be a and the units place digit be b.

Then, number is (10a + b).

According to the question:

4(a + b) + 3 = (10 a + b) 

4a + 4b + 3 = 10a + b

6a - 3b = 3

3(2a - b) = 3

2a - b =1            ... (1)

Given:

If 18 is added to the number, its digits are reversed.

The reverse of the number is (10b + a).

∴ (10a + b) + 18 = 10b + a

10a - a + b -10b = -18

9a - 9b = -18

9(a - b) = -18

a - b = -2            ... (2)

Subtracting equation (2) from equation (1):

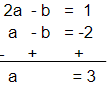
Using a = 3 in equation (1):

2(3) - b = 1

6 - b = 1

∴ b = 5

Number = 10a+b = 10 × 3 + 5 = 35