A two-digit number is obtained by either

Let the two-digit number $=10 x+y$

Case I Multiplying the sum of the digits by 8 and then subtracting $5=$ two-digit number

$\Rightarrow \quad 8 \times(x+y)-5=10 x+y$

$\Rightarrow \quad 8 x+8 y-5=10 x+y$

$\Rightarrow \quad 2 x-7 y=-5$  ...(i)

Case II Multiplyina the difference of the digits by 16 and then adding $3=$ two-digit number

$\Rightarrow \quad 16 \times(x-y)+3=10 x+y$

$\Rightarrow \quad 16 x-16 y+3=10 x+y$

$\Rightarrow \quad 6 x-17 y=-3 \quad$...(ii)

Now, multiplying in Eq. (i) by 3 and then subtracting from Eq. (ii), we get

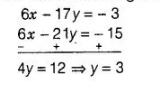
Now, put the value of $y$ in Eq. (i), we get

$2 x-7 \times 3=-5$

$\Rightarrow \quad 2 x=21-5=16 \Rightarrow x=8$

Hence the reauired two-digit number 

$=10 x+y$

$=10 \times 8+3=80+3=83$