A two-digit number is such that the product of its digits is 20. If 9 is added to the number,

Let the digits at units and tens place of the given number be $x$ and $y$ respectively. Thus, the number is $10 y+x$.

The product of the two digits of the number is 20 . Thus, we have $x y=20$

After interchanging the digits, the number becomes $10 x+y$.

If 9 is added to the number, the digits interchange their places. Thus, we have

$(10 y+x)+9=10 x+y$

$\Rightarrow 10 y+x+9=10 x+y$

$\Rightarrow 10 x+y-10 y-x=9$

$\Rightarrow 9 x-9 y=9$

$\Rightarrow 9(x-y)=9$

$\Rightarrow x-y=\frac{9}{9}$

$\Rightarrow x-y=1$

So, we have the systems of equations

$x y=20$

$x-y=1$

Here $x$ and $y$ are unknowns. We have to solve the above systems of equations for $x$ and $y$.

Substituting $x=1+y$ from the second equation to the first equation, we get

$(1+y) y=20$

$\Rightarrow y+y^{2}=20$

$\Rightarrow y^{2}+y-20=0$

$\Rightarrow y^{2}+5 y-4 y-20=0$

$\Rightarrow y(y+5)-4(y+5)=0$

$\Rightarrow(y+5)(y-4)=0$

$\Rightarrow y=-5$ Or $y=4$

Substituting the value of y in the second equation, we have

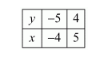
Hence, the number is $10 \times 4+5=45$.

Note that in the first pair of solution the values of x and y are both negative. But, the digits of the number can’t be negative. So, we must remove this pair.