Question:
A vertical pole fixed to the horizontal ground is divided in the ratio $3: 7$ by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a point on the ground $18 \mathrm{~m}$ away from the base of the pole, then the height of the pole (in meters) is:
Correct Option: , 2
Solution:
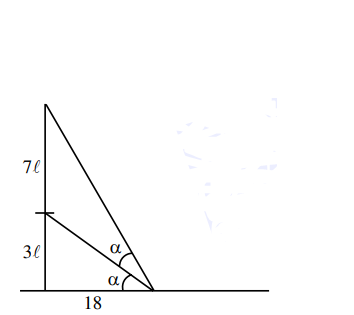
Let height of pole $=10 \ell$
$\tan \alpha=\frac{3 \ell}{18}=\frac{\ell}{6}$
$\tan 2 \alpha=\frac{10 \ell}{18}$
$\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}=\frac{10 \ell}{18}$
use $\tan \alpha=\frac{\ell}{6} \Rightarrow \ell=\sqrt{\frac{72}{5}}$
height of pole $=10 \ell=12 \sqrt{10}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
