A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long.

It is given that length of vertical stick $=6 \mathrm{~m}$

We have to find the height of the tower.

Suppose $A B$ is the height of the tower and $B C$ is its shadow.

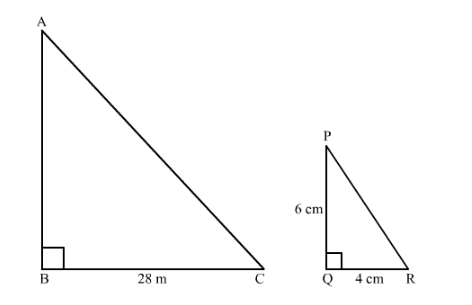
Now, $\triangle A B C \sim \triangle P C R \quad \angle B=\angle Q$ and $\angle A=\angle P$

$\frac{A B}{B C}=\frac{P Q}{Q R}$

$\frac{A B}{28} \mathrm{~m}=\frac{6}{4} \mathrm{~m}$

$\Rightarrow A B=\frac{28 \mathrm{~m} \times 6 \mathrm{~m}}{4 \mathrm{~m}}$

$\Rightarrow A B=42 \mathrm{~m}$

Hence the height of the tower is $42 \mathrm{~m}$.