A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the
bottom and the top of the flag staff are α and β respectively. Prove that the height of the tower is $\left(\frac{h \quad \tan \alpha}{\tan \beta-\tan \alpha}\right)$
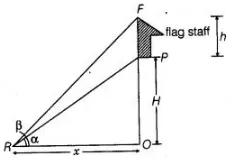
Let the height of the tower be H and OR = x
Given that, height of flag staff = h = FP and ∠PRO = α, ∠FRO = β
Now, in $\triangle P R O$, $\tan \alpha=\frac{P O}{R O}=\frac{H}{x}$
$\Rightarrow$ $x=\frac{H}{\tan \alpha}$ $\ldots(1)$
and in $\triangle F R O$, $\tan \beta=\frac{F O}{R O}=\frac{F P+P O}{R O}$
$\tan \beta=\frac{h+H}{x}$
$\Rightarrow$ $x=\frac{h+H}{\tan \beta}$ ...(ii)
From Eqs. (i) and (ii),
$\frac{H}{\tan \alpha}=\frac{h+H}{\tan \beta}$
$\Rightarrow \quad H \tan \beta=h \tan \alpha+H \tan \alpha$
$\Rightarrow \quad H \tan \beta-H \tan \alpha=h \tan \alpha$
$\Rightarrow \quad H(\tan \beta-\tan \alpha)=h \tan \alpha \Rightarrow H=\frac{h \tan \alpha}{\tan \beta-\tan \alpha}$
Hence the required height of tower is $\frac{h \tan \alpha}{\tan \beta-\tan \alpha}$
Hence proved.
