A vertical tower stands on a horizontal plane and is surmounted by a flag-staff of height 7 m

Let BC be the tower of height h m. AB be the flag staff of height 7 m on tower and D be the point on the plane making an angle of elevation of the top of the flag staff is 45° and angle of elevation of the bottom of the flag staff is 30°.

Let $C D=x, A B=7$ and $\angle B D C=30^{\circ}$ and $\angle A D C=45^{\circ}$.

We to find height of the tower

We have the corresponding figure as follows

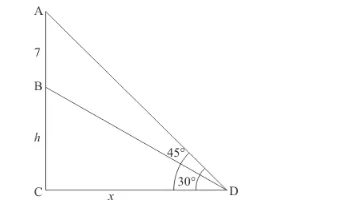
So we use trigonometric ratios.

In a triangle 

$\Rightarrow \quad \tan D=\frac{B C}{C D}$

$\Rightarrow \quad \tan 30^{\circ}=\frac{h}{x}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{x}$

$\Rightarrow \quad x=\sqrt{3} h$

Again in a triangle $A D C$

$\Rightarrow \quad \tan D=\frac{A B+B C}{C D}$

$\Rightarrow \quad \tan 45^{\circ}=\frac{h+7}{x}$

$\Rightarrow \quad 1=\frac{h+7}{x}$

$\Rightarrow \quad x=h+7$

$\Rightarrow \quad \sqrt{3} h=h+7$

$\Rightarrow h(\sqrt{3}-1)=7$

$\Rightarrow \quad h=\frac{7}{\sqrt{3}-1}$

$\Rightarrow \quad h=9.56$

Hence the height of tower is $9.56 \mathrm{~m}$.