A very long wire $A B D M N D C$ is shown in figure carrying current $I$. $A B$ and $B C$ parts are straight, long and at right angle. At $D$ wire forms a circular turn $D M N D$ of radius $R$.
$A B, B C$ parts are tangential to circular turn at $N$ and $D$. Magnetic field at the centre of circle is:
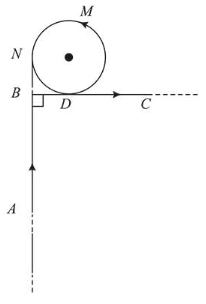
Correct Option: 1
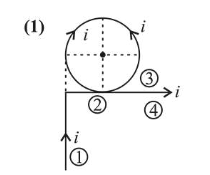
$B_{0}=B_{1}+B_{2}+B_{3}+B_{4}$
$=\frac{\mu_{0} I}{4 \pi R}\left[\sin 90^{\circ}-\sin 45^{\circ}\right]+\frac{\mu_{0} I}{2 R}+\frac{\mu_{0} I}{4 \pi R}$
$\left[\sin 45^{\circ}+\sin 90^{\circ}\right]$
$=-\frac{\mu_{0} I}{4 \pi R}\left(1-\frac{1}{\sqrt{2}}\right)+\frac{\mu_{0} I}{2 R}+\frac{\mu_{0} I}{4 \pi R}\left(1+\frac{1}{\sqrt{2}}\right)$
$\overrightarrow{\mathrm{B}_{0}^{\odot}}=\frac{\mu_{0} \mathrm{I}}{2 \pi \mathrm{R}}\left(\pi+\frac{1}{\sqrt{2}}\right)^{\odot}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.