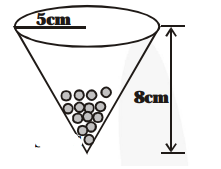
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open,

Height of the conical vessel (h) = 8 cm

Base radius (r) = 5 cm

Volume of water in conical vessel $=\frac{\mathbf{1}}{\mathbf{3}} \pi \mathrm{r}^{2} \mathrm{~h}$

$=\frac{1}{3} \times \frac{22}{7} \times(5)^{2} \times 8 \mathrm{~cm}^{3}$

$=\frac{\mathbf{4 4 0 0}}{\mathbf{2 1}} \mathrm{cm}^{3}$

Now, Total volume of lead shots

$=\frac{1}{4} \times \frac{4100}{21} \mathrm{~cm}^{3}=\frac{1100}{21} \mathrm{~cm}^{3}$

Since, radius of spherical lead shot $(\mathrm{r})=0.5 \mathrm{~cm}$

$\therefore$ Volume of 1 lead shot $=\frac{\mathbf{4}}{\mathbf{3}} \pi \mathrm{r}^{3}$

$=\frac{4}{3} \times \frac{22}{7} \times \frac{5}{10} \times \frac{5}{10} \times \frac{5}{10} \mathrm{~cm}^{3}$

$\therefore$ Number of lead shots

$=\frac{\text { Total volume of lead shots }}{\text { Vohme of } 1 \text { lead shot }}=\frac{\left[\frac{1100}{21}\right]}{\left[\frac{4 \times 22 \times 5 \times 5 \times 5}{3 \times 7 \times 1000}\right]}$

= 100

Thus, the required number of lead shots = 100.